Chapter 1 Introducción

Este capítulo presenta dos recursos que usaremos a lo largo del libro: las herramientas de desarrollo para evaluaciones en Proola.org y el software estadístico R. El capítulo finaliza con una revisión inicial de temas de estadística. Los objetivos de aprendizaje se enfocan en la comprensión de términos estadísticos, así como el cálculo y la interpretación de algunos estadísticos introductorios.

Objetivos de aprendizaje

1. Identificar y utilizar notación estadística para variables, tamaño de la muestra, promedio, desviación estándar, varianza y correlación.
2. Calcular e interpretar frecuencias absolutas, relativas y porcentuales.
3. Crear y utilizar gráficos de distribuciones de frecuencias para describir la tendencia central, variabilidad y forma de una distribución.
4. Calcular e interpretar medidas de tendencia central y describir lo que representan, incluyendo el promedio, la mediana y la moda.
5. Calcular e interpretar medidas de variabilidad y describir lo que representan, incluyendo la desviación estándar y la varianza.
6. Aplicar y explicar el proceso de escalamiento de variables utilizando la media aritmética y la desviación estándar para transformaciones lineales.
7. Calcular e interpretar la correlación entre dos variables y describir lo que ello representa en términos de forma, dirección y fuerza de la relación lineal entre variables.
8. Crear e interpretar un diagrama de dispersión y explicar lo que indica acerca de la forma, la dirección y la fuerza de la relación lineal entre dos variables.

1.1 Proola

Proola es una aplicación web para el desarrollo colaborativo de evaluaciones. Fue creado específicamente para personas que buscar practicar y disponer de ayuda en el proceso de elaboración de ítems. Tiene una interfaz simple para la creación de ítems y características para la revisión y el comentario por pate de pares.

Usted necesita configurar una cuenta gratuita en proola.org/users/sign_up antes de que pueda completar lo asignado en capítulos posteriores. Una vez que tenga una cuenta, puede comenzar a redactar y comentar los ítems.

Algunas cosas por recordar cuando comience:

• El sitio se encuentra en desarrollo, con nuevas características en camino. Para reportar fallos o enviar sugerencias, puede escribir a contact@proola.org.
• Cualquier cosa que usted comparta es pública. No publique ítems con derechos de autor, imágenes u otra información, ni tampoco los ítems que usted requiere mantener de forma segura.
• Usted puede aprender mucho a partir del éxito y el fracaso de otras personas. Busque el banco de ítems relacionado con su área de contenido, y luego vea en qué debaten las personas y cómo lo resuelven.

El proceso de elaboración de ítems con Proola se divide en 4 etapas generales (vea proola.org/learn_more).

Primero, se crea un ítem nuevo haciendo clic en “Create”, que se encuentra en la barra de navegación superior. Esto le llevará a una serie de cuadros de texto y menús desplegables donde usted brindará información básica acerca de su ítem. Como ejemplo, vea la figura 1.1. Dé un nombre corto pero descriptivo a su ítem. Luego, vincule el ítem con algún objetivo de aprendizaje. Los objetivos de aprendizaje se pueden importar de otras personas, o los puede organizar sus propios objetivos en Proola. Luego, escoja las áreas de contenido y los niveles educativos de la variedad que se le presenta. El ítem por sí mismo se compone de un encabezado, donde se ubica el enunciado o la pregunta, así como de un formato de respuestas, ya sea de elección o de construcción. Puede agregar cualquier otra información en los comentarios, una vez que haya guardado el ítem.

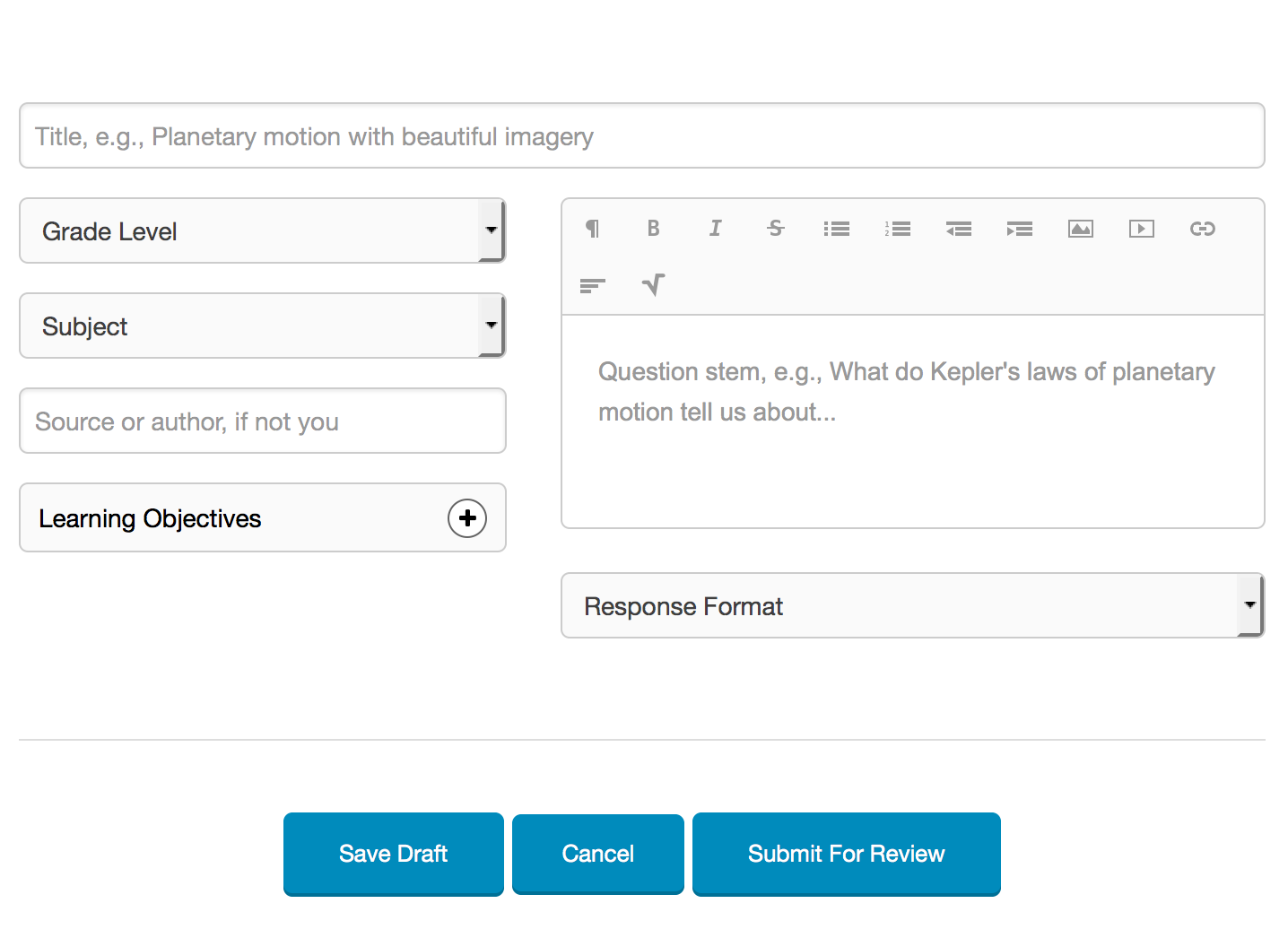
Figure 1.1: Interfaz de Proola para redactar un ítem nuevo

En segundo lugar, obtenga realimentación de pares y especialistas en evaluación. Una vez que el ítem se haya guardado como borrador, cualquiera pueder verlo y hacerle comentarios. Espere pacientemente los comentarios, o consiga personas que estén impartiendo su nivel, área de contenido, departamento, centro educativo o circuito escolar y pídales que se registren en Proola para dejar una realimentación a sus ítems. Los especialistas en evaluación incluyen integrantes de facultad o estudiantes graduados que se hayan capacitados en el desarrollo de pruebas y que puedan contribuir con la comunidad Proola. Los comentarios aparecen en una lista debajo de su ítem. Después de haberse registrado con su cuenta, vea como ejemplo, proola.org/items/439 y proola.org/items/296.

Cuando comente o responda a los comentarios de un ítem, recuerde ser constructivo. Los comentarios fluirán naturalmente hacia las limitaciones que tenga el ítem. Usted puede enfatizar tanto en las fortalezas como en las debilidades y siempre brinde sugerencias para el mejoramiento. Haga referencia a las pautas para la elaboración de ítems, ya que los ítems con algún defecto tienden a fallar en una o más de dichas pautas. Finalmente, comente acerca del alcance del ítem, esto es, qué tan bien aborda el objetivo de aprendizaje deseado con la profundidad apropiada de conocimiento.

En tercer lugar, edite y mejore sus ítems basándose en la realimentación. Enfatice en las pautas de elaboración de ítems y elija sus objetivos de aprendizaje. Apunte a la más alta profundidad en el conocimiento. Compruebe la claridad, así como que la ortografía y la gramática sean correctas.

Finalmente, envíe para revisión compartiéndolo con la comunidad. Después de enviarlo, no hay forma de retroceder. Usted y otras personas pueden comentar, pero la edición se bloquea mientras se completa la revisión formal de pares. Cuando se recomienda revisar el ítem, solo se puede editar en una nueva versión del ítem. Las versiones previas se pueden ver, pero no editar.

Revise y repita este proceso lo que sea necesario. Una vez que esté aprobado, su ítem se puede guardar, imprimir o exportar por otros usuarios.

El desarrollo de pruebas y el proceso de elaboración de ítems se abarcarán con todo detalle en el capítulo 4. Por ahora, usted debe registrarse con una cuenta y familiarizarse con la organización del sitio.

1.2 R

R es tanto un lenguaje de programación como un software para el análisis estadístico. Difiere de otros software como SPSS en tres formas principalmente. Primero, R es gratis, sin ningún compromiso o garantía. Se puede descargar de cran.r-project.org. El editor popular RStudio se encuentra también disponible en forma gratuita en rstudio.com. En segundo lugar, R es un software de código abierto, con miles de contribuyentes activos que comparten paquetes adicionales. Vea la lista completa en cran.r-project.org/web/packages (actualmente hay más de 8000 paquetes). En tercer lugar, R se accede principalmente mediante código, más que apuntando y haciendo clic en menús desplegables y ventanas de diálogo. Este tercer punto es un obstáculo para algunos, pero a la larga termina siendo una fortaleza.

En este punto usted debería descargar e instalar R y RStudio usando los vínculos dados anteriormente. En internet abundan consejos útiles sobre instalación y forma de iniciar. Aquí se dan algunas sugerencias.

• R es un software que ejecuta todos sus análisis. RStudio es un Entorno de desarrollo integrado (IDE, por sus siglas en inglés) que simplifica la interacción del usuario con R. RStudio no es esencial, pero le brinda características agradables para guardar sus códigos en R, organizar las salidas de sus análisis y administrar sus paquetes complementarios.

• Como se señaló anteriormente, se puede acceder a R vía código, en forma de comandos que se deberán digitar o pegar en la consola de R. Esta consola es simplemente una ventana donde se incluye el código de R y donde aparecen las salidas del software. Note que RStudio aparecerá con múltiples ventanas, una de las cuales será la consola de R. Esto quiere decir que, cuando aquí digamos en las instrucciones que se debe ejecutar códigos de R, esto aplica tanto para R como para RStudio.

• Cuando escriba o pegue código directamente en la consola de R, cualquier código que haya ingresado previamente aparecerá en la pantalla. En la consola, puede desplazarse por sus códigos anteriores presionando la flecha hacia arriba (en el teclado) una vez que el cursor esté frente al indicador de R >. En RStudio, también puede ver y desplazarse por una lista de comandos anteriores manteniendo presionado uno de los botones de Control/Command en su teclado mientras pulsa la flecha hacia arriba o hacia abajo.

• Únicamente puede digitar directamente en la consola para cálculos rápidos y simples de los que no le importe olvidarse. De otra manera, digite todo su código en un archivo de texto por separado de la consola. En R y en RStudio, estos archivos de texto se llaman R scripts y permiten guardar los códigos en un documento por separado, por lo que siempre tendrá una estructura guardada de lo que haya hecho. Recuerde que los R scripts se usan solo para guardar código y cualquier anotación o comentario acerca del código, pero no para datos ni para resultados.

1.2.1 Código

Comenzaremos nuestro viaje por R con un resumen de cómo los códigos se emplean para interactuar con R vía consola. En este libro, los bloques del código de R están desplazados del texto principal como se muestra a continuación. Los comentarios dentro de los bloques de código comienzan con un solo hashtag #, el código en sí mismo no tiene nada que lo preceda, y la salida de la consola de R está precedida por un doble hashtag ##. Puede copiar y pegar el código del ejemplo directamente en su consola. Cualquier cosa después del # será ignorada.

# Este es un comentario en un bloque de códigos de R. Los comentarios
# comienzan con un símbolo de hashtag y R los ignora. El código
# debajo de ese símbolo será interpretado por R una vez que usted lo pegue o #que lo digite en la consola.
x <- c(4, 8, 15, 16, 23, 42)
mean(x)  # El código que aparece después del hashtag (#) se ignora.
## [1] 18
sd(x)
## [1] 13.49074

En el código anterior, hemos creado un vector de puntuaciones x, así como hemos calculado su media aritmética o promedio y su desviación estándar. Usted puede pegar este código en la consola y verificar que obtiene los mismos resultados. Note que el código que introduce en la consola está precedido del indicador >, no así para las salidas que produce R.

Lo primero que debe notar acerca del código del ejemplo anterior es que las funciones que dan resultados en R tienen nombres y que para usarlos simplemente usamos dicho nombre y luego paréntesis, entre los cuales incluimos cualquier información o las instrucciones de cómo deberían trabajar esas funciones. Siempre que discutamos funciones en este libro, las reconoceremos por los paréntesis. Por ejemplo, usamos la función c() para combinar un conjunto de números en un “vector” de puntuaciones. La información que se suministra para usar c() consiste en las puntuaciones por sí mismas, separadas por comas. Las funciones mean() y sd() permiten obtener el promedio y la desviación estándar de los vectores, como el vector x.

Lo segundo por observar en el ejemplo anterior es que los datos y los resultados se guardan como “objetos” en R, usando el operador de asignación <-. Empleamos la función concatenar para unir nuestros números en un solo conjunto, c(4, 8, 15, 16, 23, 42), y le asignamos el nombre x al resultado. Los objetos creados de esta manera se pueden acceder después mediante el nombre que se les asignó, por ejemplo, para determinar el promedio o la desviación estándar. Si queremos acceder después a dichos cálculos, podríamos también guadar la media aritmética de x como un objeto nuevo.

# Calcular la media aritmética de x
mx <- mean(x)
# Mostrar x y su media aritmética
x
## [1]  4  8 15 16 23 42
mx
## [1] 18
print(mx)
## [1] 18

Cuando el resultado de una función se almacena en un objeto de R, usualmente no veremos ese resultado en la consola. Si digitamos el nombre del objeto en la consola, R hará lo posible para mostrar el contenido, como lo mostramos anteriormente para mx y x. Esto es simplemente un atajo para usar la función print() con un objeto de R.

Tenga en cuenta que para objetos más grandes, como marcos de datos o data.frame con muchas filas y columnas, ver todos los datos a la vez no es muy útil. En este libro analizaremos los datos del Programa Internacional para la Evaluación de Estudiantes (PISA, por sus siglas en inglés), con docenas de variables medidads para miles de estudiantes. Mostrar todos los datos de PISA inundaría la consola con información. Esto nos lleva al tercer punto por tener en cuenta sobre el código del ejemplo anterior: la consola no es el mejor lugar para ver los resultados. La consola es funcional y eficiente, pero no es bonita ni está bien organizada. Afortunadamente, R ofrece otros medios además del texto de ancho fijo para visualizar los resultados, como explicaremos a continuación.

1.2.2 Paquetes

Cuando instale R en su computadora, obtendrá una variedad de funciones y conjuntos de datos de ejemplo de forma predeterminada como parte de los paquetes básicos que vienen con R. Por ejemplo, mean() y print() son parte de los paquetes básicos de R. Los procedimientos usados comúnmente como la regresión lineal simple, vía lm(), y las pruebas t, vía t.test(), también están incluidas en esos paquetes básicos. Las funcionalidades adicionales provienen de paquetes complementarios escritos y compartidos en línea por una comunidad de entusiastas de R.

Los ejemplos de este libro se basan en unos cuantos paquetes diferentes de R. El libro en sí mismo está compilado usando los paquetes bookdown y knitr (Xie 2015; Xie 2016), y parte del código knitr se muestra para el formato de tablas de resultados. El paquete ggplot2 (Wickham 2009) se usa para elaborar gráficos. En este capítulo también necesitamos el paquete devtools (Wickham and Chang 2016), el cual nos permite instalar paquetes de R directamente desde el sitio web de código compartido github.com. Finalmente, a lo largo del libro usaremos el paquete epmr, que contiene funciones y datos que usaremos en muchos ejemplos.

Los paquetes publicados en el sitio web oficial de R llamado CRAN se instalan inicialmente utilizando install.packages(). Solo necesita hacer esto una vez por paquete. Cada vez que abra una nueva sesión de R, deberá cargar el paquete con library() para poder usarlo. De modo alternativo, puede usar funciones individuales sin cargar explícitamente un paquete, haciendo referencia tanto al paquete como a la función que va a usar, separados por ::.

Los paquetes devtools, knitr y ggplot2 están en CRAN. La versión de desarrollo del paquete epmr todavía no se encuentra en CRAN y debe instalarse usando devtools::install_github().

# Algunos ejemplos requieren datos y funciones de otros paquetes de R.
# Para instalar los paquetes que se requieren (solo se debe hacer una vez).
install.packages("devtools")
install.packages("knitr")
install.packages("ggplot2")
# Para instalar epmr desde github
devtools::install_github("talbano/epmr")

# Cargar los paquetes requeridos (se debe hacer cada vez que se reinicie R).
library("epmr")
library("ggplot2")
## 
## Attaching package: 'ggplot2'
## The following object is masked from 'package:epmr':
## 
##     alpha

Después de instalar un paquete y haber ejecutado library(), tendrá acceso a la funcionalidad del paquete. Aquí hemos cargado los paquetes epmr y ggplot2, por lo que podemos digitar las funciones directamente, sin hacer referencia al nombre del paquete cada vez que las usemos. Debido a que ambos paquetes contienen una función llamada alpha(), tendremos que hacer referencia al nombre del paquete cuando usemos esta función más adelante, en el Capítulo 5.

1.2.3 Obtener ayuda

Los archivos de ayuda en R se pueden acceder fácilmente ingresar el nombre de la función precedido del signo de cierre de interrogación, por ejemplo, ?c, ?mean, o ?devtools::install_github. No es necesario usar paréntesis. El uso del signo de interrogación es un atajo para la función help(), es decir, por ejemplo, ?mean es lo mismo que help("mean"). Cualquiera de las dos formas proporciona acceso directo a la documentación de R para una función.

La documentación de una función debería al menos brindarle una breve descripción de la función, definiciones para los argumentos que acepta la función y ejemplos de cómo utilizarla.

En la consola también puede realizar una búsqueda en toda la documentación disponible de R usando dos signos de cierre de interrogación. Por ejemplo, ??"regression" buscará en la documentación de R el término “regression”. Esto es un atajo para la función help.search(). Por último, puede navegar en la documentación de R con help.start(); esto abrirá un navegador web con enlaces a manuales y otros recursos.

Si no está satisfecho con la documentación interna de R, una búsqueda en línea puede resultar sorprendentemente efectiva para encontrar nombres de funciones o instrucciones de cómo ejecutar un determinado procedimiento o análisis en R.

1.2.4 Datos

Los datos se pueden ingresar directamente en la consola usando cualquiera de una variedad de funciones para recopilar información en forma conjunta en un objeto de R. Estas funciones generalmente le dan ciertas propiedades al objeto, tales como longitud, filas, columnas, nombres de variables y niveles de factores. En el código anterior, creamos el objeto x como un vector de puntuaciones cuantitativas, usando c(). Usted podría pensar en x como un objeto que contiene puntuaciones de una prueba para una muestra de length(x) 6 personas examinadas, sin otras variables asociadas a dichas personas.

Podemos crear un factor proporcionando un vector de valores categóricos, como texto entrecomillado, con la función factor().

# Crear una variable por factores
classroom <- c("A", "B", "C", "A", "B", "C")
classroom <- factor(classroom)
classroom[c(1, 4)]
## [1] A A
## Levels: A B C

En este código, al objeto classroom primero se le asigna un vector de letras, las cuales podrían representar etiquetas o rótulos para las tres aulas diferentes. Luego, el objeto se convierte en un factor y se le asigna un objeto del mismo nombre, lo cual esencialmente sobreescribe la primera asignación. La reutilización de nombres de objetos usualmente no se recomienda. Esto lo hicimos solo para mostrar que un nombre en R no se puede asignar al mismo tiempo a dos objetos diferentes.

El código anterior también muestra una forma simple de indexación. Los corchetes se utilizan después de algunos objetos de R para seleccionar subconjuntos de sus elementos, por ejemplo, el primer y el cuarto valor de classroom. El vector c(1, 4) se utiliza como un objeto de indexación. Tómese un minuto para practicar la indexación con x y classroom. ¿Puede mostrar las últimas tres aulas? ¿Puede mostrarlas en orden inverso? ¿Puede mostrar la primera puntuación de x tres veces?

La función data.frame() combina múltiples vectores en un conjunto de variables que se pueden visualizar y acceder como una matriz (un arreglo rectangular con filas y columnas).

# Combinar variables como columnas en un marco de datos.
mydata <- data.frame(scores = x, classroom)
mydata[1:4, ]
##   scores classroom
## 1      4         A
## 2      8         B
## 3     15         C
## 4     16         A

Podemos indexar tanto las columnas como las filas de una matriz. Debemos separar con una coma los objetos indexados. Por ejemplo, mydata[1:3, 2] mostrará las primeras tres filas de la segunda columna. mydata[6, 1:2] mostrará ambas columnas para la sexta fila. mydata[, 2], con el índice de filas vacío, mostrará todas las filas para la segunda columna. Note que la coma es necesaria aún si se omite el objeto por indexar. Tome en cuenta que los dos puntos : se emplean aquí como una función de atajo para obtener secuencias de números, donde, por ejemplo, 1:3 equivale a digitar c(1, 2, 3).

Comúnmente, importamos o cargamos datos en R, más que ingresarlos de forma manual. La importación por lo general se hace usando read.table() y read.csv(). Cada una requiere la ubicación del archivo como primer argumento. Vea la documentación de ayuda para las instrucciones de su uso y los tipos de archivos que se requieren. Los datos y cualesquiera otros objetos en la consola se pueden guardar directamente en su computadora utilizando save(). Esto crea un archivo con extensión “rda”, el cual se puede cargar nuevamente en R usando load(). Por último, algunos datos ya están disponibles en R y se pueden cargar en la sesión actual de trabajo con data(). Los datos de PISA a los que nos hemos referido antes, se pueden cargar con data(PISA09). Asegúrese de haber cargado el paquete epmr con library() antes de tratar de cargar los datos.

El objeto PISA09 es un marco de datos o data.frame que contiene variables demográficas, cognitivas y no cognitivas para un subconjunto de ítems y un subconjunto de estudiantes del estudio PISA 2009 (nces.ed.gov/surveys/pisa). Este objeto se encuentra almacenado en el paquete epmr que acompaña este libro. Después de cargar los datos, podemos mostrar algunas filas para una selección de variables, a las que se accede por su número de columna en la secuencia. Luego, mostramos los 10 primeros valores de la variable age.

# Cargar el conjunto de datos de PISA y mostrar algunos de sus subconjuntos
data(PISA09)
PISA09[c(1, 10000, 40000), c(1, 6, 7, 38)]
##       cnt   age grade  cstrat
## 1     AUS 16.00    11 -0.5485
## 10000 CAN 15.58     9  0.7826
## 40000 RUS 16.25     9  0.2159
PISA09$age[1:10]
##  [1] 16.00 16.08 16.08 15.42 16.00 15.67 16.17 15.83 15.92 15.33

El signo de dólar $ se emplea para acceder a una variable que está en un marco de datos o data.frame, a partir de su nombre. Aquí hemos mostrado la variable age, medida en años, para los primeros 10 estudiantes del conjunto de datos. Las diferentes variables de PISA09 se describirán en capítulos posteriores. Para una visión general rápida, vea el archivo de ayuda. Se puede acceder a la documentación de conjuntos de datos de la misma manera en que se accede a la documentación para funciones.

1.3 Estadística introductoria

Los hechos son cosas tercas, pero la Estadística es flexible.
— Mark Twain

Una vez expuestos los conceptos básicos de R, se encuentra listo para una revisión de la estadística introductoria que es prerrequisito para los análisis que estudiaremos posteriormente en este libro.

Muchas personas son escépticas ante las estadísticas y por buenas razones. A menudo nos encontramos estadísticas que se contradicen entre sí o que se adjuntan a afirmaciones fantasiosas acerca de la efectividad de un producto o servicio. En el fondo, la Estadística es inocente y no debería ser culpada por todos los engaños y la confusión. Las estadísticas son solo números diseñados para resumir y capturar las características esenciales de grandes cantidades de datos o información.

La Estadística es importante en la medición porque nos permite establecer puntuaciones y resumir la información recolectada con pruebas y otros instrumentos. Se utiliza para describir la fiabilidad, la validez y el poder predictivo de dicha información. También se utiliza para describir qué tan bien nuestra prueba abarca un dominio de contenido o una red de constructos, incluso en relación con otras áreas de contenido o constructos. Dependemos en gran medida de la Estadística en los Capítulos 2 y 5 con 7.

1.3.1 Algunos términos

Comenzaremos esta revisión con algunos términos estadísticos básicos. Primero, una variable es un conjunto de valores que pueden diferir para gente diferente. Por ejemplo, usualmente medimos variables tales como edad y sexo. Para distinguirlos de las palabras usuales o corrientemente utilizadas, hemos empleado cursivas para denotar que son variables estadísticas. El término variable es sinónimo de cualidad, atributo, rasgo o propiedad. Los constructos también son variables. En realidad, una variable es cualquier cosa que se le asigne a una persona y que pueda potencialmente asumir más que un solo valor constante. Como se señaló anteriormente, las variables en R pueden estar contenidas en vectores simples, por ejemplo, x, o pueden agruparse en un marco de datos o data.frame.

Las variables genéricas se etiquetarán en este libro con letras mayúsculas, usualmente, \(X\) y \(Y\). Aquí, \(X\) podría representar una puntuación en una prueba, por ejemplo, la puntuación total en todos los ítems de una prueba. También puede representar las puntuaciones en un solo ítem. En ambos casos se le considera como variable. La definición de una variable genérica como \(X\) depende del contexto en que se utilice.

También se pueden usar índices para denotar variables genéricas que forman parte de una secuencia de variables. En la mayoría de los casos, serán puntuaciones en los ítems de una prueba, donde, por ejemplo, \(X_1\) es el primer ítem, \(X_2\) es el segundo, y \(X_J\) es el último ítem, donde \(J\) corresponde a la cantidad de ítems de la prueba y \(X_j\) representa un ítem cualquiear de la secuencia. Los subíndices también se pueden usar para hacer referencia a individuos en una variable. Por ejemplo, las puntuaciones en una prueba para un grupo de personas se puede denotar por \(X_1\), \(X_2\), \(\dots\), \(X_N\), donde \(N\) es la cantidad de personas examinadas y \(X_i\) representa la puntuación para una persona genérica. Al combinar personas e ítems, tenemos que \(X_{ij}\) sería la puntuación para la persona \(i\) en el ítem \(j\).

La cantidad de personas se denota por \(n\) o, algunas veces, \(N\). Por lo general, \(n\) (minúscula) representa el tamaño de la muestra y la \(N\) (mayúscula) representa la población, sin embargo, ambas se usan indistintamente. Para otras estadísticas de muestras y poblaciones se emplean letras griegas o arábigas. El promedio de una muestra se denota por \(m\) y la media poblacional por \(\mu\), la desviación estándar es \(s\) o \(\sigma\), la varianza es \(s^2\) o \(\sigma^2\), y la correlación es \(r\) o \(\rho\). Tome en cuenta que en algunas ocasiones la media aritmética y la desviación estándar se abrevian con \(M\) and \(DE\). Esta diferenciación entre valores muestrales y poblacionales por lo general no es necesaria y empleamos los términos referidos a la población. En caso de ser necesario, se hará la identificación o aclaración que corresponda.

Finalmente, usted puede ver subíndices con nombres que se agregan a las variables y otros términos, por ejemplo, \(M_{control}\) podría indicar la media aritmética para un grupo de control. Estos subíndices dependen de la situación y deben interpretarse en su contexto.

1.3.2 Descriptiva e inferencial

Descriptiva e inferencial son términos que se refieren a dos usos generales de la Estadística. Estos usos difieren según se haga o no una inferencia a partir de las propiedades de una muestra de datos a los parámetros para una población desconocida. La Estadística descriptiva se utiliza para explorar y describir ciertas características de las distribuciones. Por ejemplo, la media y la varianza son estadísticas que identifican tendencia central y variabilidad en una distribución. Estas y otras medidas estadísticas se usan de manera inferencial cuando se hace una generalización a la población que contiene la muestra en que se calculan.

Los descriptivos no suelen utilizarse para responder preguntas de investigación o informar para la toma de decisiones. En cambio, las estadísticas inferenciales son más apropiadas para esto, al ser menos exploratorias y más confirmatorias.

Las estadísticas inferenciales implican una inferencia a un parámetro o valor poblacional. La calidad de esta inferencia se mide utilizando pruebas estadísticas que hacen referencia al error asociado a nuestras estimaciones. En esta revisión nos enfocaremos en las estadísticas descriptivas. Más adelante consideraremos algunas aplicaciones inferenciales.

La función dstudy() del paquete epmr calcula algunas estadísticas descriptivas univariadas usadas comúnmente, que incluyen la media, la mediana, la desviación estándar (sd), la asimetría (skew), la curtosis (kurt), el mínimo (min) y el máximo (max). Cada una de ellas se discutirá más adelante. La función dstudy() también determina la cantidad de personas de la muestra (n) y la cantidad de personas con datos faltantes (na).

# Obtener estadísticas descriptivas para tres variables de PISA09.
dstudy(PISA09[, c("elab", "cstrat", "memor")])
## 
## Descriptive Study
## 
##            mean  median   sd   skew kurt   min  max     n na
## elab   -0.12099  0.0385 1.03 -0.181 3.38 -2.41 2.76 44265  0
## cstrat  0.04951 -0.0411 1.02 -0.408 4.69 -3.45 2.50 44265  0
## memor   0.00151  0.1036 1.03 -0.218 4.23 -3.02 2.69 44265  0

Verificación de aprendizaje: ¿Cuál es la principal diferencia entre estadística descriptiva y estadística inferencial?

1.3.3 Distribuciones

Una variable para una muestra dada se puede resumir contando la cantidad de personas que tienen los mismos valores entre sí. El resultado es una distribución de frecuencias, donde el total de personas es una frecuencia absoluta denotada por \(f\). Por ejemplo, la variable categórica \(X\) representa el color de ojos y puede tener tres valores distintos en un aula de \(n=20\) estudiantes: azul, café y verde. Una distribución de frecuencias absolutas simplemente sumaría la cantidad de estudiantes con cada color de ojos, por ejemplo, \(f_{azul} = 8\).

Si la frecuencia absoluta se divide por el tamaño de la muestra, obtenemos una frecuencia relativa (proporción). Por ejemplo, \(p_{azul} = f_{azul}/n\). Multiplicando ese resultado por 100, se obtiene una frecuencia porcentual (porcentaje). Estos tipos de frecuencias describen la misma información para los valores dentro de una distribución, pero de formas ligeramente diferentes.

Veamos algunas frecuencias en los datos de PISA. La primera variable en PISA09, llamada cnt, se clasifica como un factor en R, y contiene el país de cada estudiante examinado. Podemos revisar la clase y luego usar table() para tener las frecuencias de la cantidad de examinados en cada país.

# Revisar la clase de la variable país y crear una tabla de frecuencias.
class(PISA09$cnt)
## [1] "factor"
table(PISA09$cnt)
## 
##  AUS  BEL  CAN  DEU  ESP  GBR  HKG  ITA  JPN  RUS  SGP  USA 
## 4334 2524 7125 1420 7984 3717 1484 9551 1852 1638 1638 1611

Para expresar las frecuencias absolutas por país como porcentajes, podemos dividir los resultados de la tabla generada por la cantidad de estudiantes, esto es, la cantidad de filas de la tabla en PISA09 y luego multiplicar por 100. Asimismo, podemos redondear los resultados a 2 decimales, utilizando round(). Esto indica el porcentaje de estudiantes en cada país en relación con todos los estudiantes \(N =\) 44878.

# Convierta una tabla de frecuencias por país en porcentajes y luego redondee el resultado a 2 decimales.
cntpct <- table(PISA09$cnt) / nrow(PISA09) * 100
round(cntpct, 2)
## 
##   AUS   BEL   CAN   DEU   ESP   GBR   HKG   ITA   JPN   RUS   SGP   USA 
##  9.66  5.62 15.88  3.16 17.79  8.28  3.31 21.28  4.13  3.65  3.65  3.59

Verificación de aprendizaje: ¿Cuál es la suma de todas las frecuencias en una distribución? ¿Cuál es la suma de una distribución de frecuencias relativas y de frecuencias porcentuales?

Los gráficos de barras y los histogramos son representaciones visuales de las distribuciones de frecuencias; un gráfico de barras muestra una barra por cada frecuencia y un histograma puede juntar algunas barras para mejorar la interpretación con variables continuas, es decir, variables donde las personas no calzan en un conjunto discreto de categorías. Un gráfico de barras funciona mejor con una variable categórica como país. Para variables continuas como PISA09$memor, resulta más apropiado usar un histograma. memor es una de las escalas de puntuación producidas por PISA. Mide el grado en que los estudiantes reportan el uso de estrategias de memorización cuando leen para comprender un texto.

# Crea un gráfico de barras para la cantidad de estudiantes por país.
ggplot(PISA09, aes(cnt)) + geom_bar(stat = "count")
# Los histogramas son más apropiados para variables o puntuaciones continuas.
qplot(PISA09$memor, binwidth = .5)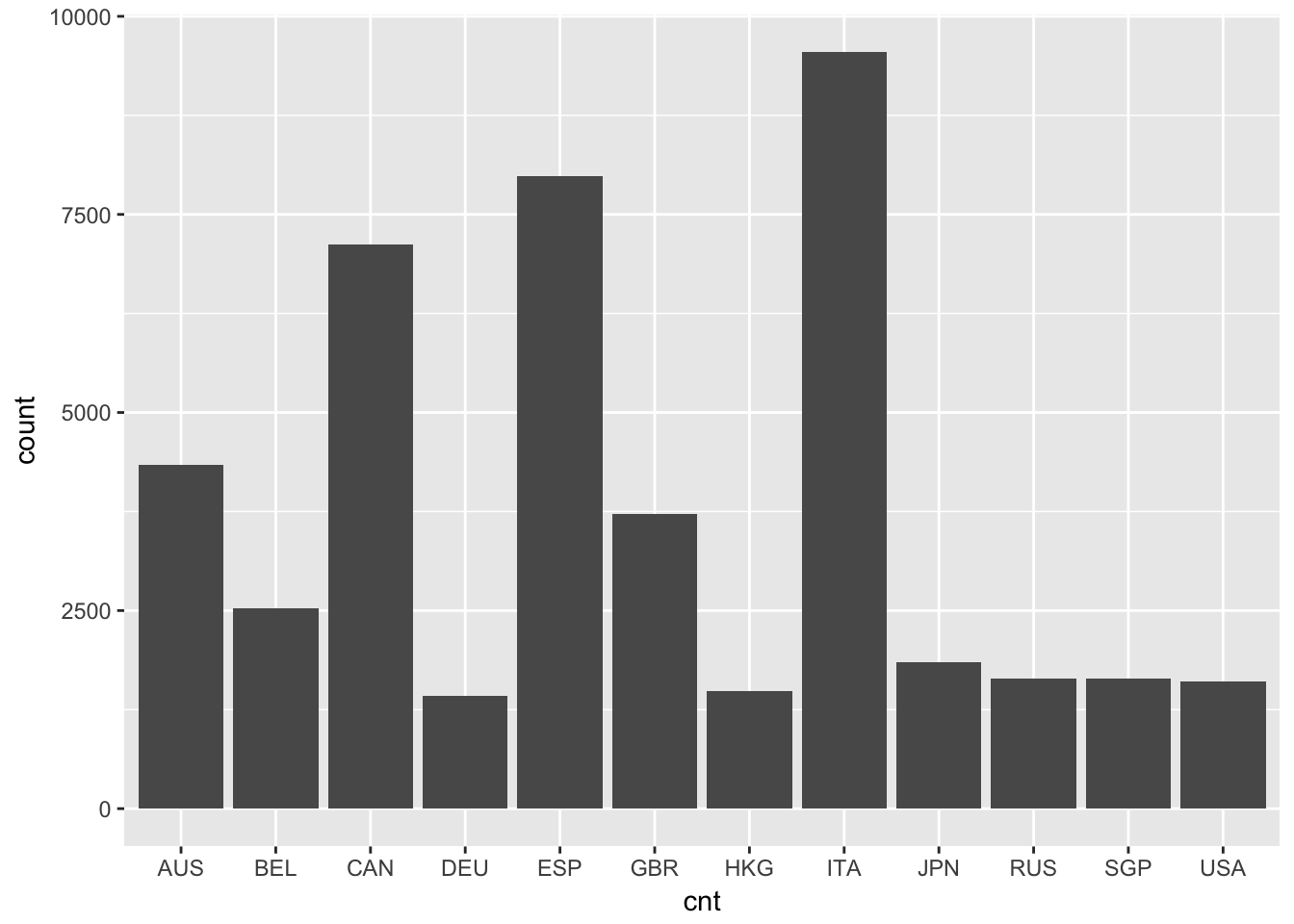

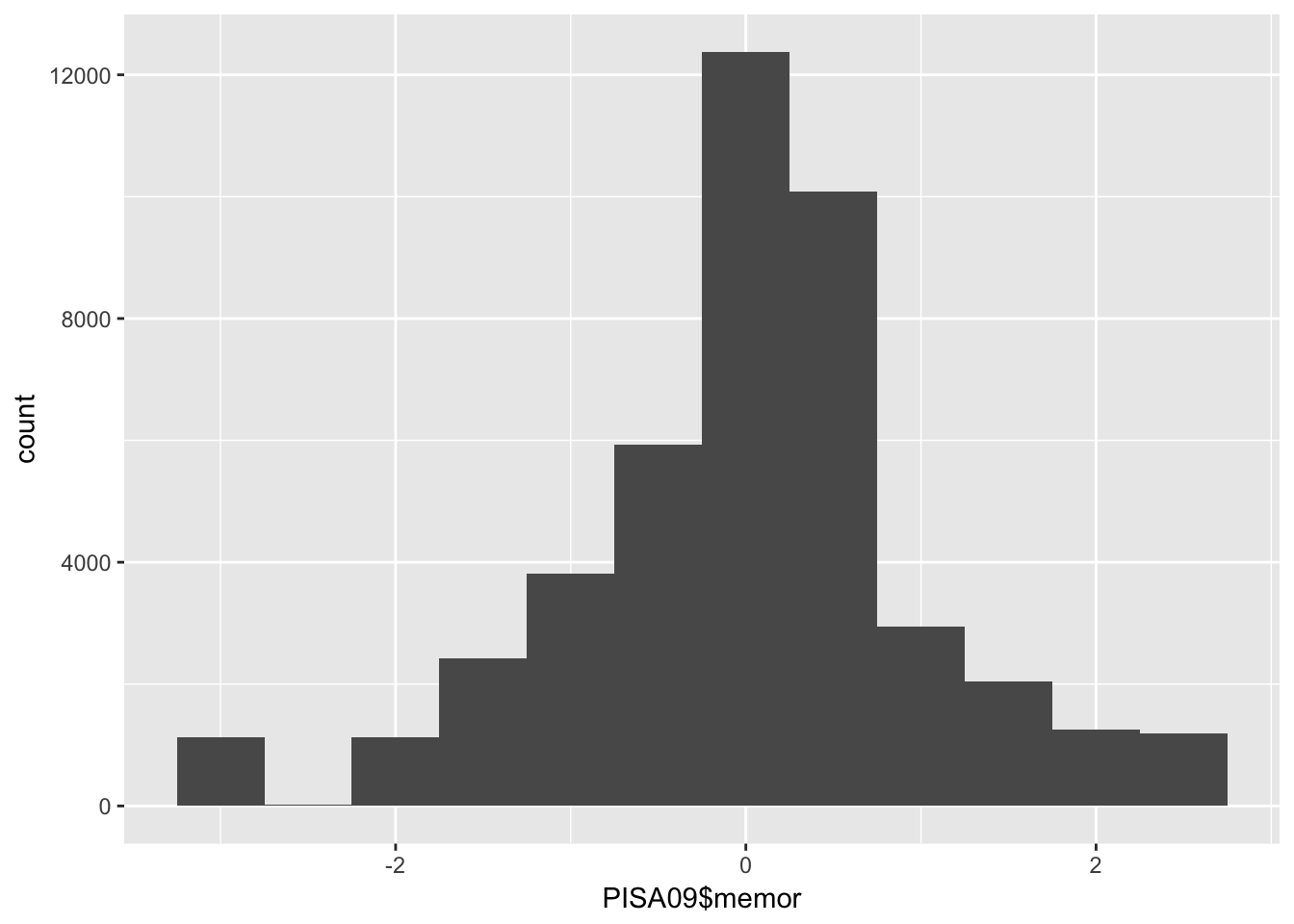
Figure 1.2: A bar plot of student frequencies by country in the first plot, and a histogram of memor scores in the second.

Un gráfico de caja, también conocido como un gráfico de caja y bigotes, muestra una distribución de puntuaciones utilizando cinco estadísticas de resumen: el mínimo, el primer cuartil (corresponde al 25% de las personas que están por debajo de la puntuación), el segundo cuartil (la mediana o el percentil 50), el tercer cuartil (corresponde al 75% de las personas que están por debajo de la puntuación), y el máximo. En R, estas estadísticas se pueden obtener usando summary(). La caja captura el rango intercuartil y los bigotes se extienden aproximadamente hasta los valores mínimo y máximo; los valores atípicos se indican usualmente con puntos. Aquí usamos gráficos de caja para comparar las distribuciones en las puntuaciones de la variable memor por país.

# Crea una serie de gráficos de caja para las puntuaciones en la variable memor por país.
ggplot(PISA09, aes(cnt, memor)) + geom_boxplot()

Tenga en cuenta que estas funciones para elaboración de gráficos proceden del paquete ggplot2. Como alternativa, el paquete base contiene barplot(), hist() y boxplot(), las cuales también funcionarán. No necesita comprender todos los detalles de la sintaxis para graficar, pero debería poder modificar el código del ejemplo dado aquí para examinar las distribuciones de otras variables.

Algunas distribuciones tienen formas particulares. Por ejemplo, una distribución con las mismas o muy similares cantidades de personas en cada valor, se considera como una distribución uniforme. Grafique la distribución de la variable PISA09$age y verá un buen ejemplo de esto. Una distribución se llama distribución normal cuanto cierta cantidad de ella se ubica en el punto central. Por ejemplo, en una distribución normal, aproximadamente el 68 % de las puntuaciones debe estar a una unidad de desviación estándar a partir de la media y las frecuencias deberían decrecer e ir disminuyendo conforme se alejan del centro. Una distribución que disminuya hacia la izquierda pero no hacia la derecha se describe como asimétrica negativa, mientras que la que disminuye hacia la derecha pero no hacia la izquierda se describe como asimétrica positiva. Finalmente, una distribución que es más alta que la normal se llama leptocúrtica, con curtosis alta, y una distribución que es más alta que la normal es platicúrtica, con curtosis baja.

Verificación de aprendizaje: Describa las diferencias entre un gráfico de barras y un histograma, con ejemplos de cuándo utilizar cada uno de ellos.

1.3.4 Tendencia central

Las medidas de tendencia central brindan estadísticas que describen la mitad, el valor más común o el valor más normal en una distribución. La media aritmética o promedio es técnicamente apropiada solo para variables medidas por intervalo o razón y representa la puntuación que está más cerca de todas las demás puntuaciones. La media también representa el punto de balance en una distribución, de modo que cuanto más lejos esté la puntuación del centro, mayor será lo que se desplace la media hacia una dirección determinada. La media para una variable \(X\) es simplemente la suma de todas las puntuaciones \(X\) dividida por el tamaño de la muestra:

\[\begin{equation} \mu = \frac{\sum_{i=1}^{n}X_i}{n} \tag{1.1} \end{equation}\]

La mediana es la puntuación de la mitad en una distribución, la puntuación que divide la distribución en dos partes con la misma cantidad de personas en cada lado. La moda simplemente es la puntuación o las puntuaciones con las mayores frecuencias.

La media aritmética o promedio es por mucho la medida de tendencia central más popular, en parte porque es la base de muchas otras medidas estadísticas, incluyendo la desviación estándar, la varianza y la correlación. Como resultado, el promedio también es la base de la regresión y el ANOVA.

En R, podemos hallar fácilmente el promedio con mean() y la mediana con median() para un vector de puntuaciones. Como no hay función base para calcular la moda, examinaremos una tabla de frecuencias para hallar los valores más comunes.

Cuando usemos ciertas funciones en R, tales como mean() y sd(), tendremos que indicarle a R cómo trabajar con los datos faltantes. Esto usualmente puede hacerse con el argumento na.rm. Por ejemplo, con na.rm = TRUE, R no considerará a las personas con datos faltantes al hacer los cálculos.

Verificación de aprendizaje: Explique cómo se puede esperar que los valores atípicos de diferentes magnitudes influyan en la media, la mediana y la moda.

1.3.5 Variabilidad

La variabilidad describe la cantidad de puntuaciones que se distribuyen o que difieren entre sí en una distribución. Algunas medidas simples de variabilidad son el mínimo y el máximo, que en conjunto capturan el rango de puntuaciones para una variable.

# Verifique el mínimo, el máximo y el rango para la variable age.
min(PISA09$age)
## [1] 15.17
max(PISA09$age)
## [1] 16.33
range(PISA09$age)
## [1] 15.17 16.33

La varianza y la desviación estándar son medidas de variabilidad mucho más útiles ya que nos dicen cuánto varían las puntuaciones. Ambas se definen en función de la variabilidad con respecto a la media. Como resultado, ambas son técnicamente apropiadas solo para variables medidas en escalas de intervalo o razón, las cuales se analizarán en el Capítulo 2.

La varianza es la distancia cuadrática media para cada puntuación con respecto al promedio, o la suma de las distancias cuadráticas con respecto a la media dividida por el tamaño de la muestra menos 1:

\[\begin{equation} \sigma^2 = \frac{\sum_{i=1}^{n}(X_i - \mu)^2}{n - 1} \tag{1.2} \end{equation}\]

Dado que la varianza se expresa como un valor cuadrático, su métrica es la de una puntuación cuadrática, por lo que generalmente no tiene mucho uso práctico. Como resultado, la varianza a menudo no se examina ni se reporta como una estadística independiente. En su lugar, se toma la raíz cuadrada para obtener la desviación estándar:

\[\begin{equation} \sigma = \sqrt{\frac{\sum_{i=1}^{n}(X_i - \mu)^2}{n - 1}} \tag{1.3} \end{equation}\]

La desviación estándar se interpreta como la distancia promedio con respecto a la media y se expresa en la métrica de la puntuación bruta, lo que hace que sea más fácil de interpretar. La desviación estándar de sd(PISA09$age) 0.292078 indica que los estudiantes de PISA09 varían en promedio alrededor de 0.3 años, es decir, 3.5 meses.

# Verifique las desviaciones estándar en un ítem para Hong Kong (HKG) y # Alemania (DEU) 
sd(PISA09$st33q01[PISA09$cnt == "HKG"], na.rm = TRUE)
## [1] 0.6891664
sd(PISA09$st33q01[PISA09$cnt == "DEU"], na.rm = TRUE)
## [1] 0.9060628

Verificación de aprendizaje: En el ítem st33q01 de PISA, las desviaciones estándar para los estudiantes de Hong Kong (HKG) y de Alemania (DEU) fueron 0.69 y 0.91, respectivamente. Compare y contraste esos resultados. En ese ítem, los estudiantes puntuaron su nivel de acuerdo (1 = totalmente en desacuerdo hasta 4 = totalmente de acuerdo) con el enunciado: “El centro educativo ha hecho poco para prepararme para la vida adulta cuando salga de la escuela.”

1.3.6 Correlación

La covariabilidad, similar a la variabilidad, describe cuánto las puntuaciones se distribuyen o difieren entre sí, pero toma en cuenta qué tan similiares son estos cambios para cada persona de una variable a otra. A medida que los cambios son más consistentes entre las personas, la covariabilidad aumenta. La covariabilidad se estima con mayor frecuencia utilizando la covarianza y la correlación.

La covariabilidad se calcula utilizando dos distribuciones de puntuación, que se denominan como distribución bivariada de puntuaciones. La covarianza es el equivalente bivariado de la varianza para una distribución univariada y se calcula de la misma manera:

\[\begin{equation} \sigma_{XY} = \frac{\sum_{i=1}^{n}(X_i - \mu_X)(Y_i - \mu_Y)}{n - 1} \tag{1.4} \end{equation}\]

Tenga en cuenta que ahora tenemos dos variables diferentes: \(X\) y \(Y\) y que las medias se etiquetan de acuerdo con ello. La covarianza a menudo se denota por \(\sigma_{XY}\).

Al igual que la varianza, la covarianza no es muy útil en sí misma porque se expresa en términos de productos de puntuaciones, en vez de hacerlo en la métrica más familiar de puntuaciones brutas. Sin embargo, la raíz cuadrada de la covarianza no nos ayuda porque hay dos métricas de puntuaciones brutas involucradas en el cálculo. La correlación resuelve este problema eliminando, o dividiendo por completo estas métricas:

\[\begin{equation} \rho_{XY} = \frac{\sigma_{XY}}{\sigma_X \sigma_Y} \tag{1.5} \end{equation}\]

Al dividir la covarianza por el producto de las desviaciones estándar de \(X\) y \(Y\), obtenemos una medida de la relación entre ellas que no tiene una métrica de puntuaciones brutas que se pueda intepretar. La correlación varía entre -1 y 1. Una corelación de 0 indica que no hay una relación lineal entre las variables, mientras que -1 o 1 indican una relación lineal perfecta entre ellas.

En R, cov() y cor() se utilizan para obtener covarianzas y correlaciones. Cuando solo tenemos dos variables, las separamos con una coma. Para obtener la covarianza o la correlación de dos o más combinaciones diferentes de variables, podemos proporcionar una matriz o un marco de datos (data.frame).

# Obtener la covarianza y la correlación para variables diferentes.
# El argumento use especifica cómo proceder con los datos faltantes.
# Vea ?cor para más detalles.
cov(PISA09$age, PISA09$grade, use = "complete")
## [1] 0.02163678
cor(PISA09[, c("elab", "cstrat", "memor")],
  use = "complete")
##             elab    cstrat     memor
## elab   1.0000000 0.5126801 0.3346299
## cstrat 0.5126801 1.0000000 0.4947891
## memor  0.3346299 0.4947891 1.0000000

El argumento use = "complete" se emplea para obtener covarianzas o correlaciones basadas únicamente en personas con datos en todas las variables.

Las correlaciones se usan comúnmente para indexar la intensidad y dirección de la relación lineal entre dos variables. Las correlacioens pequeñas y moderadas entre tres escalas de estrategias de aprendizaje nos dicen que hay algunas relaciones lineales entre ellas. Los gráficos de dispersión nos ayudan a visualizar estas relaciones. La figura 1.3 muestra un diagrama de dispersión para dos variables de estrategias de aprendizaje de estudiantes en los Estados Unidos de América. Se excluyó a los demás países por simplicidad.

# Diagrama de dispersión para dos variables de estrategias de aprendizaje
# geom_point() agrega los puntos al gráfico.
# position_jitter() los mueve un poco para dejar al descubierto las
# densidades de puntos que de otro modo se superpondrían.
ggplot(PISA09[PISA09$cnt == "USA", ], aes(elab, cstrat)) +
  geom_point(position = position_jitter(w = 0.1, h = 0.1))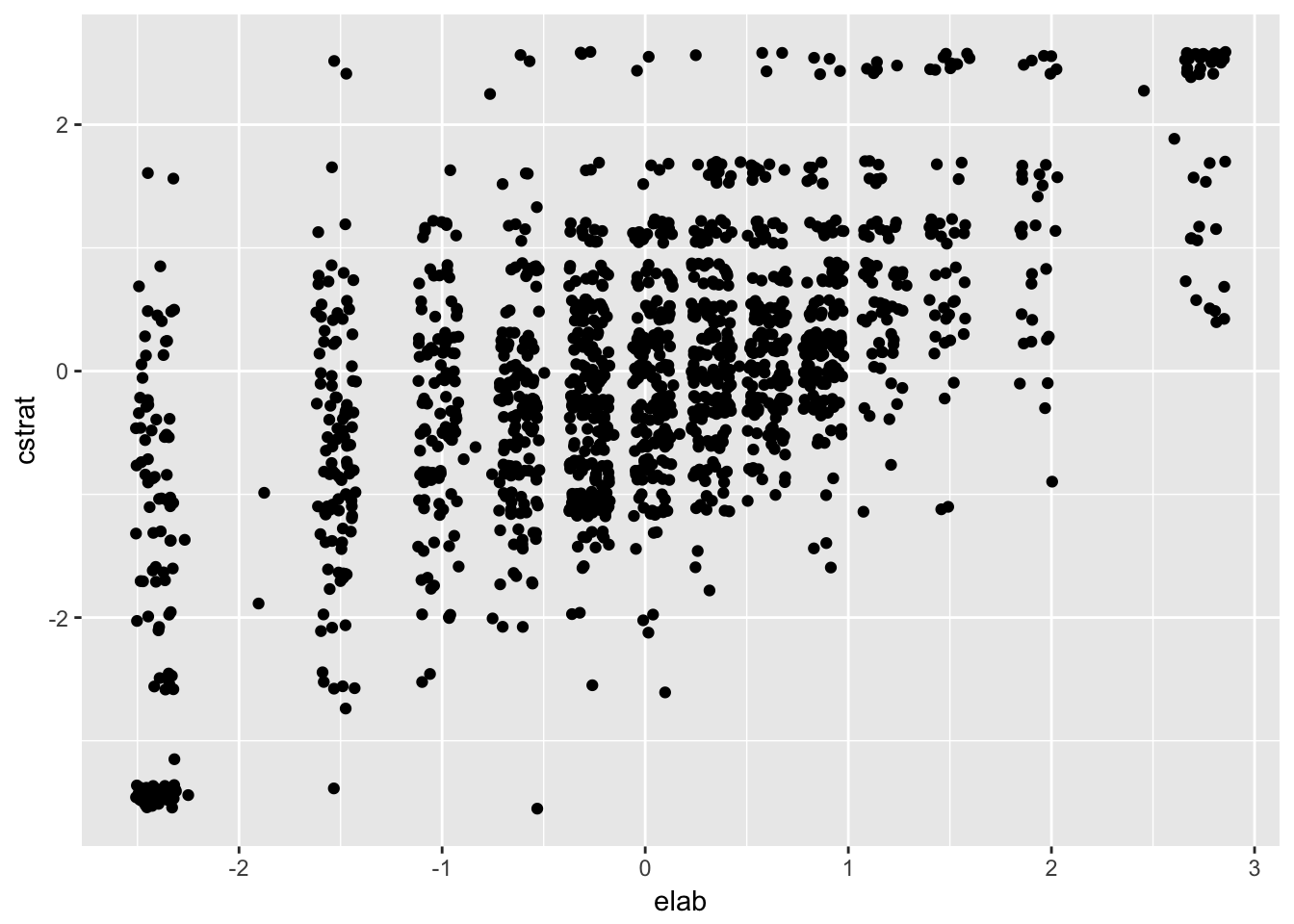

Figure 1.3: Diagrama de dispersión para las escalas de estrategias de aprendizaje elab y cstrat en PISA para EEUU.

Las correlaciones positivas indican que, en general, a medida que aumentan las puntuaciones en una varialbe, también tienden a aumentar en la otra variable. Las correlaciones más fuertes indican, en general, hasta qué punto esto es cierto. En la figura 1.3, las puntuaciones de una variable difieren sustancialmente para valores dados en la otra. Por ejemplo, las puntuaciones de cstrat abarcan casi todo el eje y para puntuaciones de elab por debajo de -1. Esto representa una inconsistencia en la puntuación, relativa a la media, de una variable con respecto a otra.

Tenga en cuenta que PISA09$cnt == "USA" se usa en el código anterior como un objeto de indexación para seleccionar únicamente filas para estudiantes de los EEUU. Usted puede crear objetos de indexación en R usando operadores de comparación. Por ejemplo, == pregunta si cada valor de la izquierda es igual que un valor simple en la derecha. El resultado de un vector de clase logical, que contiene los valores TRUE (verdadero) y FALSE (falso). Con una variable logical como índice, se omite cualquier fila que sea FALSE, mientras que se mantienen aquellas filas que correspondan a TRUE. Otras comparaciones incluyen > para mayor que y <= para menor o igual que. Vea ?Comparison para más detalles.

Verificación de aprendizaje: Compare y contraste las correlaciones de -0.40 y 0.60 en términos de fuerza y dirección de la relación lineal que mide cada una de ellas.

1.3.7 Reescalamiento

Las variables a menudo se modifican para tener ciertas propiedades, incluyendo intervalos de puntuación más pequeños o más grandes, así como diferentes puntos medios y diferente variabilidad. Un ejemplo común es la escala de puntuación-\(z\), que se define para tener una media de 0 y una desviación estándar de 1. Cualquier variable que tenga un promedio y una desviación estándar se puede convertir en puntuaciones-\(z\), que expresan cada puntuación en términos de distancias con respecto a la media en unidades de desviación estándar. Una vez que una escala se ha convertido a la métrica de puntuación \(z\), se puede transformar para tener cualquier punto medio, a través de la media y cualquier factor de escala, a través de la desviación estándar.

Para convertir una variable \(Y\) de su escala de puntuación original a una escala de puntuaciones-\(z\), tendremos que restar \(\mu_Y\) (la media de \(Y\)), de cada puntuación y luego dividirla por \(\sigma_Y\) (la desviación estándar de \(Y\)), esto es:

\[\begin{equation} Y_z = \frac{Y - \mu_Y}{\sigma_Y} \tag{1.6} \end{equation}\]

Al restar la media de cada puntuación, la media de la nueva variable \(Y_z\) es 0, y al dividir cada puntuación por la desviación estándar, la desviación estándar de la nueva variable es 1. Ahora podemos multiplicar \(Y_z\) por cualquier constante \(s\) y luego sumar o restar cualquier otra constante \(m\) para obtener una variable transformada linealmente, con media \(m\) y desviación estándar \(s\). La nueva variable reescalada la designaremos con \(Y_r\):

\[\begin{equation} Y_r = Y_z\text{s} + \text{m} \tag{1.7} \end{equation}\]

La transformación lineal de cualquier variable \(Y\) con respecto a su métrica original, con media aritmética \(\mu_Y\) y desviación estándar \(\sigma_Y\), a una escala definida por una nueva media y desviación estándar, se obtiene mediante la combinación de estas dos ecuaciones:

\[\begin{equation} Y_r = (Y - \mu_Y)\frac{\text{s}}{\sigma_Y} + \text{m} \tag{1.8} \end{equation}\]

Las transformaciones de escalas a menudo se emplean en pruebas por una de dos razones. En primer lugar, las transformaciones se pueden usar para expresar una variable en términos de un promedio familiar y una desviación estándar. Por ejemplo, las puntuaciones de CI se expresan tradicionalmente en una escala con media aritmética 100 y desviación estándar de 15. En este caso, la Ecuación (1.8) se usa con \(\text{m} = 100\) y \(\text{s} = 15\). Otra escala popular de puntuación se conoce como la escala \(t\), con \(\text{m} = 50\) y \(\text{s} = 10\). En segundo lugar, las transformaciones se pueden usar para expresar una variable en términos de una métrica nueva y única. Cuando en el año 2011 se revisó el GRE (www.ets.org/gre) se creó una nueva escala de puntuaciones, en parte para desalentar las comparaciones directas con versiones previas de dicho examen. Las antiguas escalas GRE de razonamiento cuantitativo y verbal oscilaron entre 200 y 800 puntos y las versiones revisadas ahora varían entre 130 y 170.

Vamos a transformar PISA09$age en puntuaciones-z. Luego, haremos un reescalamiento para obtener un nuevo promedio y una nueva desviación estándar. Usted debería verificar el promedio y la desviación estándar para cada variable indicadas en el siguiente código y compararlas con los valores originales. Note que R algunas veces representa el cero como una cantidad infinitamente pequeña, usando notación científica, en vez de solo reportar 0.

# Convierta la variable age en puntuaciones-z, luego haga un reescalamiento para obtener un nuevo promedio y una nueva desviación estándar.
# Usted debería verificar la media aritmética y la desviación estándar tanto para zage como para newage.
# También vea setmean() y setsd() del paquete epmr, y scale()
# de la base de R.
zage <- (PISA09$age - mean(PISA09$age)) / sd(PISA09$age)
newage <- (zage * 150) + 500

El reescalamiento que utiliza sumas/restas y divisiones/multiplicaciones, como se muestra aquí, se conoce como transformación lineal. Cuando transformamos una variable, la forma de la distribución no cambia. Las transformaciones lineales solo afectan los valores en el eje x. Por este motivo, se usan comúnmente solo para propósitos de interpretación.

# Histogramas de la variable age y la versión reescalada de la variable age
ggplot(PISA09, aes(factor(round(zage, 2)))) + geom_bar()
ggplot(PISA09, aes(factor(round(newage, 2)))) + geom_bar()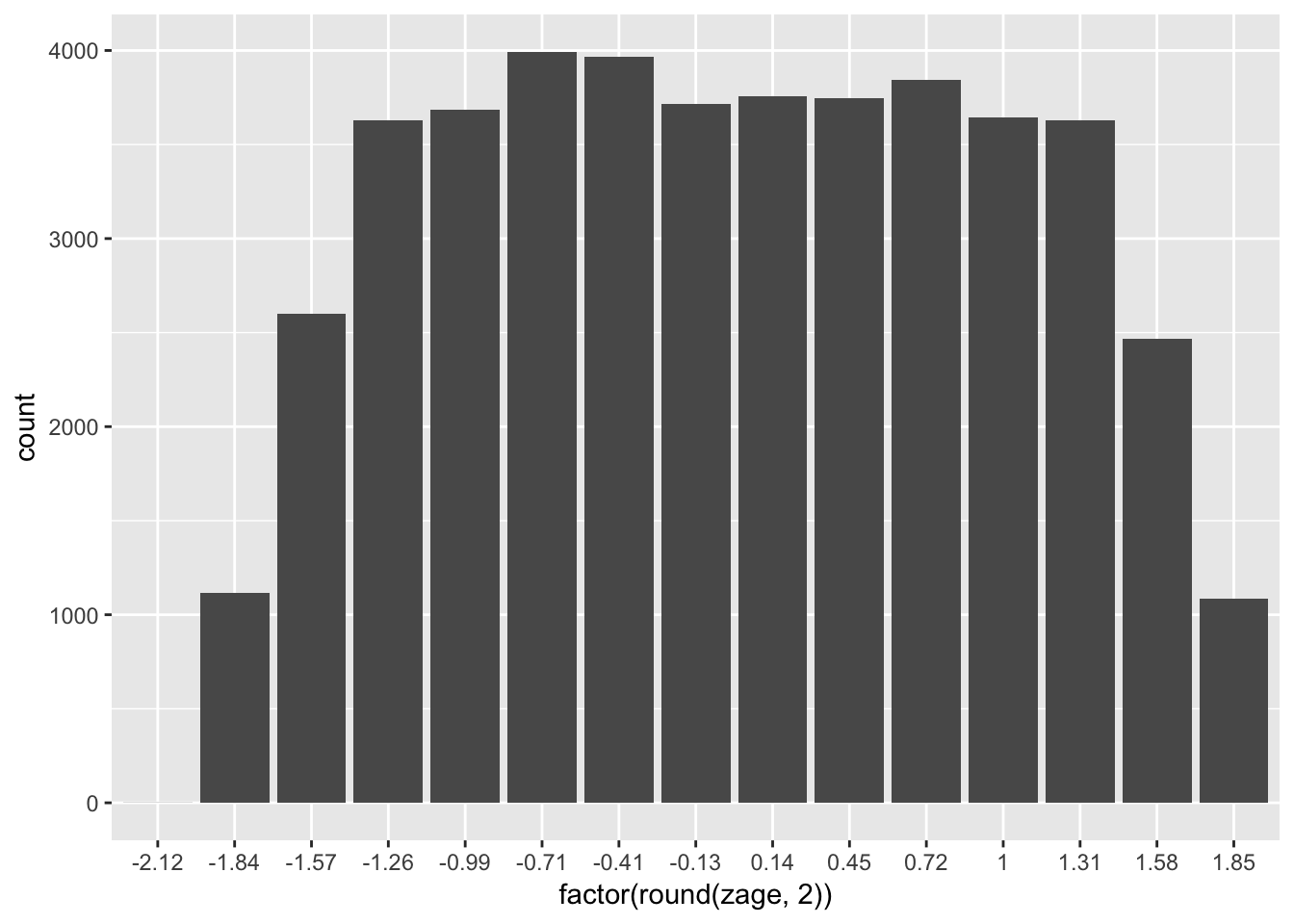

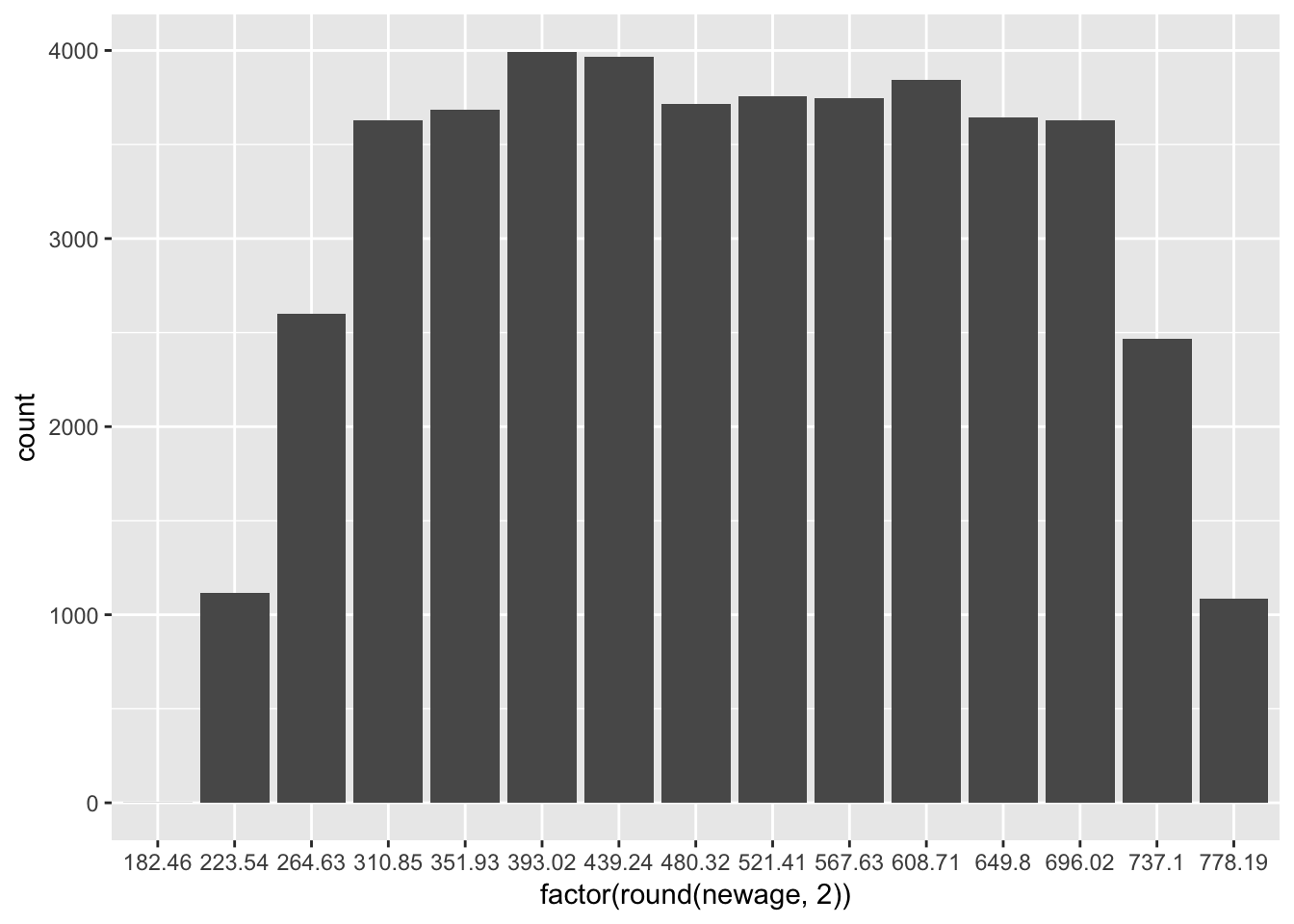
Figure 1.4: Histogramas de la variable age en el primer gráfico y la edad reescalada con una media de 500 y una desviación estándar de 150, en el segundo gráfico.

Verificación de aprendizaje: Resuma, con ejemplos, las dos razones para transformar linealmente una escala de puntuaciones.

1.4 Resumen

Este capítulo introdujo dos recursos que se utilizarán en este libro: Proola y R. También se revisaron algunos conceptos estadísticos intoductorios, lo que apoyará nuestras discusiones acerca de fiabilidad, análisis de ítems, teoría de respuesta a los ítems, dimensionalidad y validez.

Antes de avanzar, usted debería tener una cuenta en Proola y revisar el banco de ítems. También debería instalar R en su computadora y, opcionalmente, instalar RStudio, y asegurarse de que se siente cómodo acerca la explicación de distribuciones de frecuencias, tendencia central, variabilidad, correlación y reescalamiento, incluyendo qué son y cuándo utilizarlos.

1.4.1 Ejercicios

1. Determine las estadísticas descriptivas para la variable age utilizando dstudy(). ¿Cuál es la edad promedio? ¿Cuál es la edad mayor reportada en el conjunto de datos de PISA? Confirme estos resultados con las funciones mean() y max() de la base de R.
2. Reporte la distribución de frecuencias para PISA09$grade como una tabla. ¿Cuál es la proporción de estudiantes que están en décimo año?
3. Elabore un gráfico de barras para la variable age usando el código de ggplot() que aparece encima de la figura 1.2, reemplazando cnt por age. No olvide agregar + geom_bar(stat = "count"), el cual especifica que las barras representan frecuencias. ¿Cuántos estudiantes tienen exactamente 16 años de edad? Usted puede verificar estos resultados utilizando table(). Note que, aunque age es una variable continua, se midió en PISA usando valores discretos.
4. Encuentre la media aritmética, la mediana y la moda para el ítem st33q01 de PISA “actitud hacia el centro educativo”, para Alemania y Hong Kong. Interprete esos valores para cada país. En este ítem, los estudiantes calificaron su nivel de acuerdo (1 = totalmente en desacuerdo hasta 4 = totalmente de acuerdo) con el enunciado: “El centro educativo ha hecho poco para prepararme para la vida adulta cuando salga de la escuela.”
5. ¿Cómo se comparan los países JPN y RUS en términos de sus puntuaciones promedio en memoria (memor)? Note que el promedio internacional entre todos los países es 0.
6. Describa la variabilidad de las calificaciones del ítem st33q01 de PISA. ¿Los estudiantes están reportando niveles similares de acuerdo o varían en sus calificaciones?
7. La variable PISA09$bookid identifica el folleto de examen o la forma de la prueba que recibió un estudiante en esta submuestra del conjunto de datos completo de PISA. ¿Cuántos folletos se usaron? ¿Cuántos estudiantes recibieron cada folleto?
8. ¿Cuál de las escalas de estrategias de aprendizaje tiene la mejor distribución normal de puntuaciones? ¿Cuál información respalda su elección? Reporte sus resultados.
9. PISA09$r414q02s y PISA09$r414q11s contienen las puntuaciones en dos ítems de lectura en PISA, donde 1 corresponde a la respuesta correcta y 0 a la incorrecta. Encuentre e inteprete la correlación entre estas dos variables.
10. Elabore un vector de puntuaciones con rango de 0 a 10. Encuentre la media aritmética y la desviación estándar de esas puntuaciones. Luego, conviértalas a la métrica CI, con una media aritmética de 100 y una desviación estándar de 15.

References

Xie, Yihui. 2015. Bookdown: Authoring Books with R Markdown. https://github.com/rstudio/bookdown.

Xie, Y. 2016. knitr: A General-Purpose Package for Dynamic Report Generation in R. R package version 1.12.3.

Wickham, Hadley. 2009. ggplot2: Elegant Graphics for Data Analysis. New York, NY: Springer.

Wickham, Hadley, and Winston Chang. 2016. devtools: Tools to Make Developing R Packages Easier. https://CRAN.R-project.org/package=devtools.