Posted on

Visualizing Conditional Standard Error in the GRE

Below is some R code for visualizing measurement error across the GRE score scale, plotted against percentiles. Data come from an ETS report at https://www.ets.org/s/gre/pdf/gre_guide.pdf.

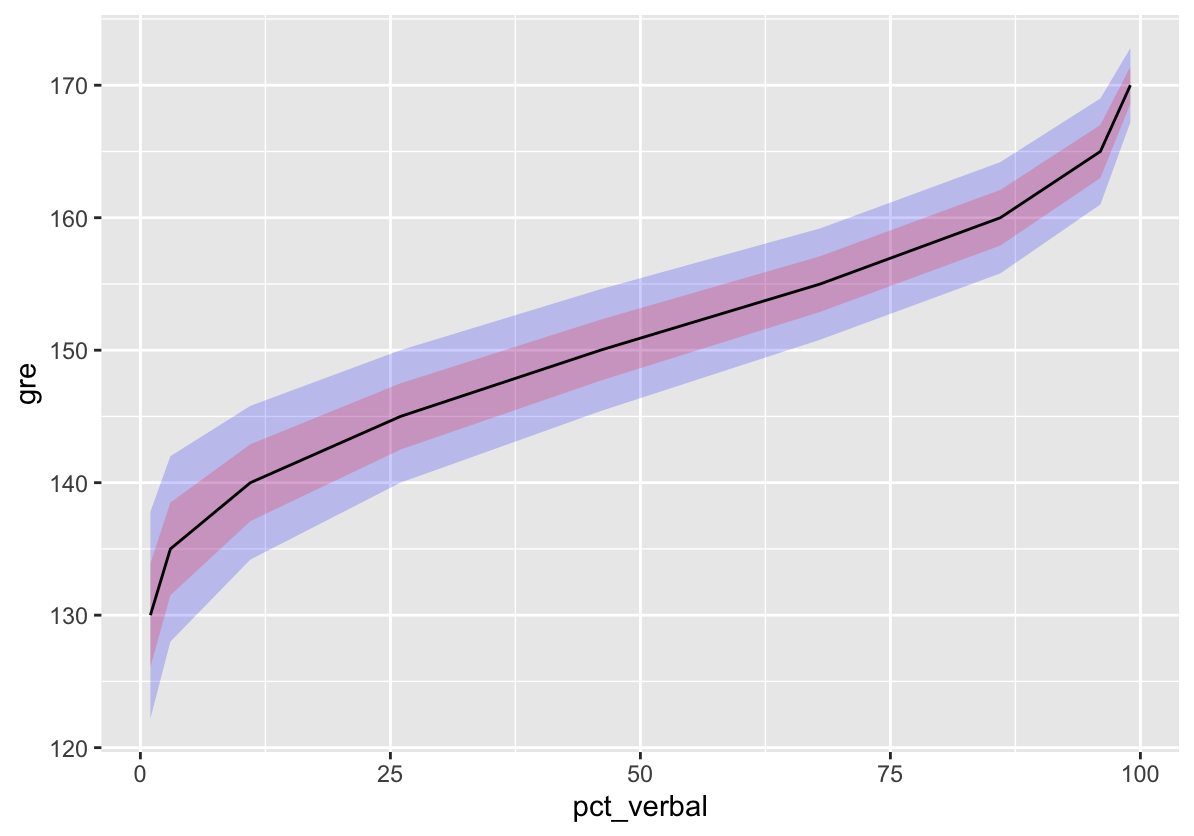
The plot shows conditional standard error of measurement (SEM) for GRE verbal scores. SEM is the expected average variability in scores attributable to random error in the measurement process. For details, see my last post.

Here, the SEM is conditional on GRE score, with more error evident at lower verbal scores, and less at higher scores where measurement is more precise. As with other forms of standard error, the SEM can be used to build confidence intervals around an estimate. The plot has ribbons for 68% and 95% confidence intervals, based on +/- 1 and 2 SEM.

# Load ggplot2 package
library("ggplot2")

# Put percentiles into data frame, pasting from ETS
# report Table 1B
pct <- data.frame(gre = 170:130,
matrix(c(99, 96, 99, 95, 98, 93, 98, 90, 97, 89,
  96, 86, 94, 84, 93, 82, 90, 79, 88, 76, 86, 73,
  83, 70, 80, 67, 76, 64, 73, 60, 68, 56, 64, 53,
  60, 49, 54, 45, 51, 41, 46, 37, 41, 34, 37, 30,
  33, 26, 29, 23, 26, 19, 22, 16, 19, 13, 16, 11,
  14, 9, 11, 7, 9, 6, 8, 4, 6, 3, 4, 2, 3, 2, 2,
  1, 2, 1, 1, 1, 1, 1, 1, 1),
  nrow = 41, byrow = T))

# Add variable names
colnames(pct)[2:3] <- c("pct_verbal", "pct_quant")

# Subset and add conditional SEM from Table 5E
sem <- data.frame(pct[c(41, seq(36, 1, by = -5)), ],
  sem_verbal = c(3.9, 3.5, 2.9, 2.5, 2.3, 2.1, 2.1,
    2.0, 1.4),
  sem_quant = c(3.5, 2.9, 2.4, 2.2, 2.1, 2.0, 2.1,
    2.1, 1.0),
  row.names = NULL)

# Plot percentiles on x and GRE on y with
# error ribbons
ggplot(sem, aes(pct_verbal, gre)) +
  geom_ribbon(aes(ymin = gre - sem_verbal * 2,
    ymax = gre + sem_verbal * 2),
    fill = "blue", alpha = .2) +
  geom_ribbon(aes(ymin = gre - sem_verbal,
    ymax = gre + sem_verbal),
    fill = "red", alpha = .2) +
  geom_line()
Posted on

Confidence Intervals in Measurement vs Political Polls

In class this week we covered reliability and went through some examples of how measurement error, the opposite of reliability, can be converted into a standard error for building confidence intervals (CI) around test scores. Students are often surprised to learn that, despite a moderate to strong reliability coefficient, a test can still introduce an unsettling amount of error into results.

Measurement

Here’s an example from testing before I get to error in political polling. The GRE verbal reasoning test has an internal consistency reliability of 0.92, with associated standard error of measurement (SEM) of 2.4 (see Table 5A in this ETS report).

Let’s say you get a score of $X = 154$ on the verbal reasoning test. This puts you in the 64th percentile among the norming sample (Table 1B). We can build a CI around your score as

$$CI = X \pm SEM \times z$$

or

$$CI = 154 \pm 2.4 \times 1.96$$

where the z of 1.96 comes from the unit normal curve.

After rounding, we have a range of about 10 points within which we’re 95% confident your true score should fall. That’s 154 – 4.3 = 149.7 at the bottom (41st percentile after rounding) and 154 + 4.3 = 158.3 at the top (83rd percentile after rounding).

I’ll leave it as an exercise for you to run the same calculations on the analytical writing component of the GRE, which has a reliability of 0.86 and standard error of 0.32. In either case, the CI will capture a significant chunk of scores, which calls into question the utility of tests like the GRE for comparisons among individuals.

I should mention that the GRE is based on item response theory, which presents error as a function of the construct being measured, where the SEM and CI would vary over the score scale. The example above is simplified to a single overall reliability and SEM.

Polling

Moving on to political polls, Monmouth University is reporting the following results for democratic candidate preference from a phone poll conducted this week with 503 prospective voters in New Hampshire (full report here).

  1. Sanders with 24%
  2. Buttigieg with 20%
  3. Biden with 17%
  4. Warren with 13%

This is the ranking for the top four candidates. Percentages decrease for the remaining choices.

Toward the end of the article, the margin of error is reported as 4.4 percentage points. This was probably found based on a generic standard error (SE), calculated as

$$SE = \frac{\sqrt{p \times q}}{\sqrt{n}}$$

or

$$\frac{\sqrt{.5 \times .5}}{\sqrt{503}}$$

where p is the proportion (percentage rating / 100) that produces the largest possible variability and SE, and q = 1 – p. This gives us SE = 0.022 or 2.2%.

The 4.4, found with $SE \times 1.96$, is only half of the confidence interval. So, we’re 95% confident that the actual results for Sanders fall between 24 – 4.4 = 19.6% and 24 + 4.4 = 28.4%, a range which captures the result for Buttigieg.

All of the point differences for adjacent candidates in the rankings, which are currently being showcased by major news outlets, are within this margin error.

Note that we could calculate SE and confidence intervals that are specific to the percentages for each candidate. For Sanders we get an SE of 1.9%, for Buttigieg we get 1.8%. We could also use statistical tests to compare points more formally. Whatever the approach, we need to be more clear about the impacts of sampling error and discuss results like these in context.